|
HOME
ESR
EXPERIMENTS
LABS etc
|
|
E121
E127
E132
E125
E143
laser_cooling_2021
E142
Ê128
E146
E0052
E0018
E0028
E0038
E0075
E0203_E0018
E0052_2025
E0281 - NEEC
|
| proton-capture on 118Te |
Not logged in |
 |
|
|
 Wed Apr 29 16:06:28 2020, Laszlo, Calibration, efficiency fit - 90degree, combined dataset, Wed Apr 29 16:06:28 2020, Laszlo, Calibration, efficiency fit - 90degree, combined dataset,  
|
 Thu Apr 30 17:40:57 2020, Laszlo, Calibration, efficiency fits, Thu Apr 30 17:40:57 2020, Laszlo, Calibration, efficiency fits,   
|
 Thu Apr 30 22:55:45 2020, Laszlo, Calibration, inverse square law test, Thu Apr 30 22:55:45 2020, Laszlo, Calibration, inverse square law test, 
|
 Wed May 6 23:02:42 2020, Laszlo, Calibration, efficiency values, Wed May 6 23:02:42 2020, Laszlo, Calibration, efficiency values,  
|
|
|
Message ID: 278
Entry time: Wed Apr 29 16:06:28 2020
Reply to this: 279
|
| Author: |
Laszlo |
| Category: |
Calibration |
| Subject: |
efficiency fit - 90degree, combined dataset |
| Year: |
|
|
|
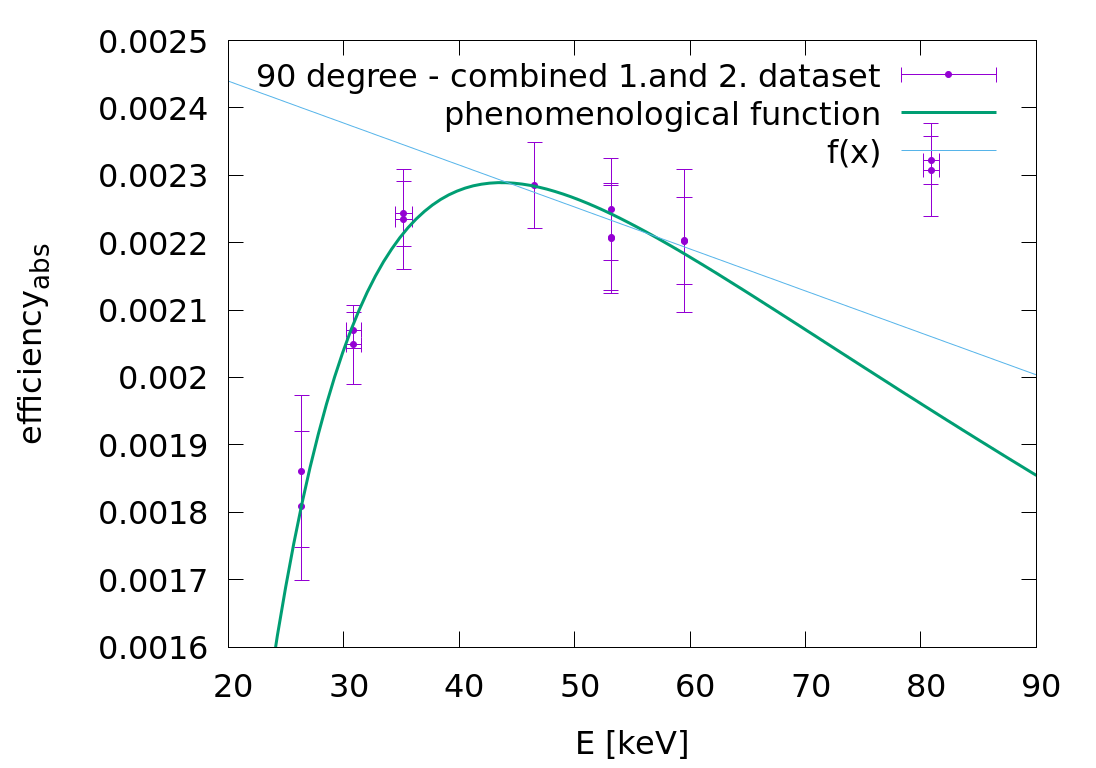
For the efficiency vs E fit of the 90degree Xray detector I have used the following phenomenological funciton:
f(x) = a * (1-exp(-(x-c)/b)) * exp(-x/d)
Here the first exponent member is a saturation curve. This part describes the passing through of the two Be windows (chamber + before detector) and through the dead layer of Ge crystal. One needs a minimum energy to enter to the detecting Ge crystal = C parameter. b parameter = characteristic absorbtion E of these nondetecting layers.
The second exponent is an exponential decrease of the detector efficiency. Photons with higher energy are less detectable by the germaniums. The d parameter is the characteristic E for hard Xray and gamma (>40keV) detectability.
https://www.amptek.com/internal-products/si-pin-vs-cdte-comparison
//Jan's comment: the tail of this function should more or less follow a linear trend a bit above than 40 keV.
In the attachment there is an example fit for 90 degree with combined 1. and 2. (before and after beamtime) calibration datasets.
I made the fit with gnuplot:
degrees of freedom (FIT_NDF) : 8
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.419915
variance of residuals (reduced chisquare) = WSSR/ndf : 0.176329
p-value of the Chisq distribution (FIT_P) : 0.994094
Final set of parameters Asymptotic Standard Error
======================= ==========================
a = 0.00308376 +/- 0.0005144 (16.68%)
c = 15.6259 +/- 2.035 (13.03%)
b = 9.36888 +/- 3.16 (33.73%)
d = 177.141 +/- 84.95 (47.95%)
Laszlo's out. |
|
|
|