Table of ion energies calculated from cooler parameters
|
nominal energy | V_set | V_meas | I_set | E_ion | E_Error
| |
6 MeV/u | 3460.5 V | 3364 V | 50 mA | 6.042 MeV/u | YY keV/u
| |
7 MeV/u | 4008.3 V | 3913 V | 50 mA | 7.049 MeV/u | YY keV/u
|
Here is how the calculation works:
1. Find the voltage and current set values that were active during the measurement cycle.
2. These are only SetValues. For the current this is fine, but for the voltage you have to subtract an offset. This offset comes from the power supply and changes over time. It is measured regularly and the present offset you have to inquire with the ESR/cooler crew. For our beam time E127b in 2021 the offset is:
V_offset = -95 +/- ?? V (only for E127b)
The uncertainty has still to be discussed.
3. The space charge of the electron beam reduces the effective voltage seen by the electrons and thus reduces their energy. You have to calculate the space charge potential Phi_0 on the beam axis using the following formular:
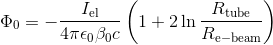
using R_tube = 10cm and R_e-beam = 2,54 cm and all constants, you arrive at the ESR specific equation:
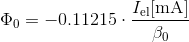
4. Now calculate effective Voltage and electron energy:
V_eff = V_set + V_offset + Phi_0
This time we measured the effective voltage for each energy, so we can actually use this values (V_meas) instead of V_set + V_offset.
E_e = e * V_eff
5. With E_e you can now calculate the ion energy by using the definition of the Lorentzfactor gamma:
gamma - 1 = E_kin/(m_0 * c^2)
In equilibrium, the left side of the equation is equal for both, electrons and ions in the cooler, leading to:
E_ion = E_el * M_ion/M_el
which gives the total energy of the ions.
NOTE:
In principle, this should be an iterative calculation, since the potential depends on beta and is then used to calulate beta or ion energy. But in practice a single iteration is precise enough, if beta was a good estimate. |